Multivariate Analysis Lecture 14: More on Classification

Zhaoxia Yu | Professor, Department of Statistics

2025-05-14

Introduction

Code 
knitr::opts_chunk$set(echo = TRUE)
library(tidyr) #the pipe (%>%) tool is extremely useful
library(MASS)
library(ggplot2)
library(kableExtra)
library("gridExtra")
library(klaR) #visualize lda and qda
library(knitr)

Outline

  • Review of LDA
  • QDA
  • Decision theory
    • Equal costs
    • Unequal costs

Review of LDA

Linear Discrminant Analysis

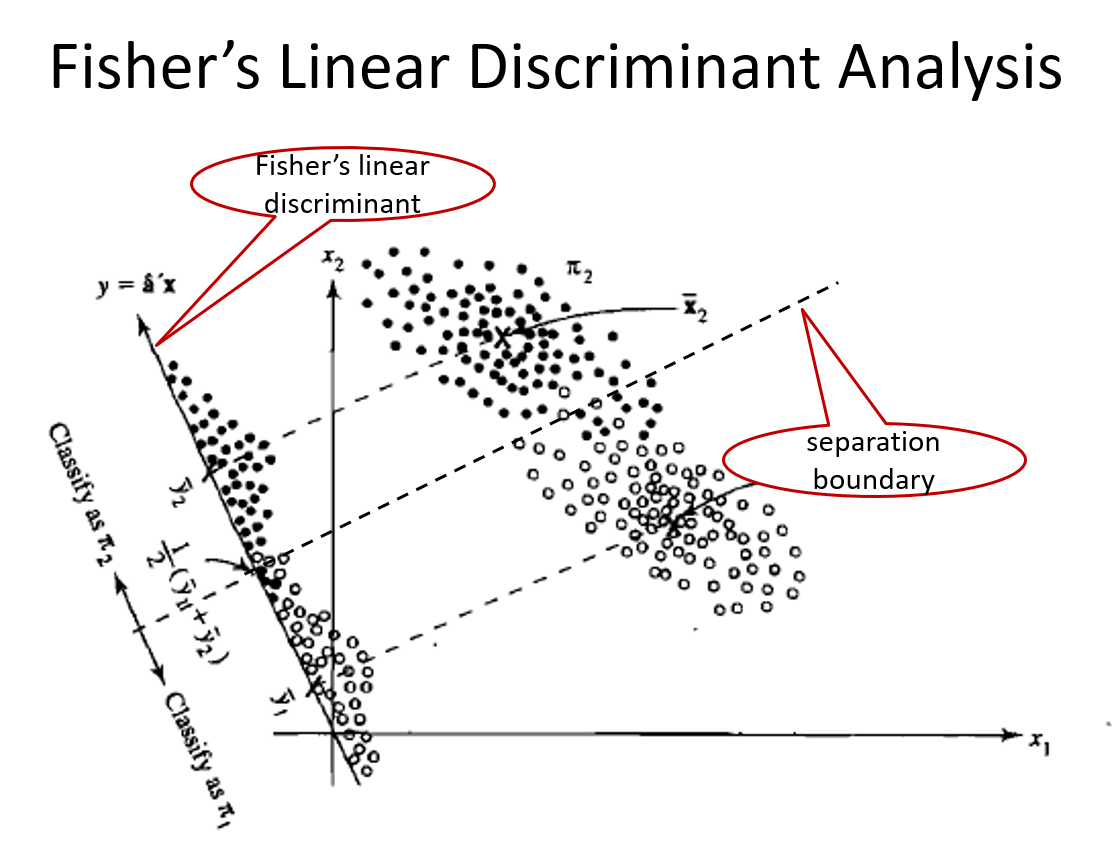
FLDA: Maximum Separability for Two-Class Problems

  • The maximization problem is \[\operatorname*{argmax}_a \frac{a^T(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)^Ta}{a^T \boldsymbol \Sigma a}\]

  • Use an argument similar to PCA, such \(a\) is the first eigenvector of \(\boldsymbol \Sigma ^{-1}(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)^T\).

  • We can show that \(a=\mathbf S_p^{-1}(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)\).

  • The linear function \[f(x)=a^T x \mbox{ where } a=\mathbf S_p^{-1}(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)\] is called Fisher’s linear discriminant function.

Allocate New Observations

  • Consider an observation \(X_0\). We compute \[f(X_0)=a^T X_0\] where \(a=\mathbf S_p^{-1}(\bar {\mathbf X}_1 - \bar {\mathbf X}_2)\)

  • Let \[m=a^T \frac{\bar {\mathbf X}_1 + \bar {\mathbf X}_2}{2}=\boldsymbol (\bar {\mathbf X}_1 - \bar {\mathbf X}_2)^T \mathbf S_p^{-1}\frac{\bar {\mathbf X}_1 + \bar {\mathbf X}_2}{2}\]

  • Allocate \(X_0\) to

    • class 1 if \(f(X_0)>m\)
    • class 2 if \(f(x_0)<m\)

g-Class Problems

  • Measure separation using F statistic \[\begin{aligned} F(a) &= \frac{MSB}{MSW}=\frac{SSB/(g-1)}{SSW/(n-g)}\\ &= \frac{\sum_{i=1}^g n_i (\bar Y_{i.}^{(1)} -\bar Y_{..}^{(1)})^2/(g-1)}{\sum_{i=1}^g (n_i-1)S_{Y_i^{(1)}}^2/(n-g)}\\ &=\frac{a^T \sum n_i (\bar X_{i.} -\bar X_{..})(\bar X_{i.}-\bar X_{..})^T a}{a^T \sum_{i=1}^g\sum_{j=1}^{n_i} (X_{ij} -\bar X_{i.})(X_{ij}-\bar X_{i.})^T a}\frac{n-g}{g-1}\\ &= \frac{a^T \mathbf B a}{a^T \mathbf W a}\frac{n-g}{g-1} \end{aligned}\] where \(n=\sum_{i=1}^g n_i\), \(\mathbf B\) is the between-group sample covariance matrix, and \(\mathbf W\) is the within-group sample covariance matrix.

Linear Discriminants

  • The first linear discriminant is the linear function that maximizes \(F(a)\). It can also be shown that the first linear discriminant is given by the first eigenvector of \(\mathbf W ^{-1} \mathbf B\), i.e., \[Y_{ij}^{(1)}=\gamma_1^T X_{ij}\] where \(\gamma_1\) is the first eigenvector of \(\mathbf W ^{-1} \mathbf B\).

  • Similarly, for \(k=1, \cdots, rank(\mathbf B)\), the \(k\)th linear discriminant is given by the \(k\)th eigenvector of \(\mathbf W ^{-1} \mathbf B\)

  • \[Y_{ij}^{(k)}=\gamma_k^T X_{ij}\]

Use the Linear Discriminants

  • Let \(X_0\) be a new observation. We allocate it to the group with the minimum distance defined by the Euclidean distance in space spanned by the linear discriminants.

  • Calculate \(Y_0^{(k)}=\gamma_k^T X_0\), the projection of \(X_0\) to the \(k\)th linear discriminant for \(k=1, \cdots, rank(B)\).

  • Calculate the distance between \((Y_0^{(1)}, \cdots, Y_0^{(rank(B))})\) and \((\bar Y_{i.}^{(1)}, \cdots, \bar Y_{i.}^{(rank(B))})\)

\[D^2(X_0, i) = \sum_{k=1}^{rank(B)} [Y_0^{(k)} - \bar Y_{i.}^{(k)}]^2\]

  • Allocate \(X_0\) to \(\operatorname*{argmin}_i D^2(X_0, i)\).

Quadratic DA (QDA)

QDA for Two-Class Problems

  • The LDA can be derived using likelihood functions under the assumptions
    1. Multivariate normal
    2. Equal covariance matrix
  • The assumption of equal covariance matrix is not always a good approximation to the true covariance matrices
  • If we relax this assumption, we will have QDA

QDA for Two-Class Problems

  • Let’s consider a two-class classification problem with \(n_1\) and \(n_2\) observations in classes 1 and 2, respectively.

  • Suppose we have two independent random samples

    • Sample 1: \(X_{1j}\overset{iid}\sim N(\mathbf \mu_1, \boldsymbol \Sigma_1)\), where \(j=1, \cdots, n_1\)
    • Sample 2: \(X_{2j}\overset{iid}\sim N(\mathbf \mu_2, \boldsymbol \Sigma_2)\), where \(j=1, \cdots, n_2\)

  • Sample mean vectors: \[\bar {\mathbf X}_1=\frac{1}{n_1}\sum_{j=1}^{n_1}X_{1j}, \bar {\mathbf X}_2=\frac{1}{n_2}\sum_{j=1}^{n_2}X_{2j}\]

  • Remark: the sample mean vectors are the MLE of the corresponding mean vectors

QDA for Two-Class Problems

  • MLE of covariance matrices \[\hat {\boldsymbol\Sigma}_1 = \frac{n_1-1}{n_1}S_1, \hat {\boldsymbol\Sigma}_2 = \frac{n_2-1}{n_2}S_2\] where \(S_i\) is the sample covariance matrix for sample \(i\).

  • Likelihood functions \[\begin{aligned} L_1(\boldsymbol \mu_1, \boldsymbol \Sigma_1) \propto |\boldsymbol\Sigma_1|^{-1/2} exp\{-\frac{1}{2} (x-\boldsymbol \mu_1)^T \boldsymbol \Sigma_1^{-1} (x-\boldsymbol \mu_1)\}\\ L_2(\boldsymbol \mu_2, \boldsymbol \Sigma_2) \propto |\boldsymbol\Sigma_2|^{-1/2} exp\{-\frac{1}{2} (x-\boldsymbol \mu_2)^T \boldsymbol \Sigma_2^{-1} (x-\boldsymbol \mu_2)\} \end{aligned}\]

QDA for Two-Class Problems

  • We can either check whether the ratio is greater than one or check whether the difference of log-likelihood is positive.

\[l_1 - l_2=-\frac{1}{2}log(\frac{|\boldsymbol\Sigma_1|}{|\boldsymbol\Sigma_2|}) - \frac{1}{2} [(x-\boldsymbol \mu_1)^T \boldsymbol \Sigma_1^{-1} (x-\boldsymbol \mu_1) - (x-\boldsymbol \mu_2)^T \boldsymbol \Sigma_2^{-1} (x-\boldsymbol \mu_2)]\]

  • The classification boundary is given by \(l_1-l_2=0\), i.e.,

\[(x-\boldsymbol \mu_1)^T \boldsymbol \Sigma_1^{-1} (x-\boldsymbol \mu_1) - (x-\boldsymbol \mu_2)^T \boldsymbol \Sigma_2^{-1} (x-\boldsymbol \mu_2) = log(\frac{|\boldsymbol\Sigma_2|}{|\boldsymbol\Sigma_1|})\]

  • It is quadratic!

QDA for Two-Class Problems

  • Replace unknown parameters with estimate, we have the classification rule: allocate \(x\) to class 1 if \[(x-\bar {\mathbf X}_1)^T \mathbf S _1^{-1} (x-\bar {\mathbf X}_1) - (x-\bar {\mathbf X}_2)^T \mathbf S_2^{-1} (x-\bar {\mathbf X}_2) < log(\frac{|\mathbf S_2|}{|\mathbf S_1|})\]

QDA for g-Class Problems

  • For the \(i\)th group, we compute a quadratic score, which is defined as
    \[Q_i(x)=(x-\bar {\mathbf X}_i)^T \mathbf S _i^{-1} (x-\bar {\mathbf X}_i)+ log(|\mathbf S_i|)\]

  • Allocate \(x\) to the class with the minimum quadratic score

Example of QDA

Code 
obj.lda=lda(Species~., data = iris)
obj.qda=qda(Species~., data = iris)

table(Pred=predict(obj.lda, iris)$class,
True=iris$Species)
table(Pred=predict(obj.qda, iris)$class,
True=iris$Species)

Example of QDA

            True
Pred         setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         1
  virginica       0          2        49
            True
Pred         setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         1
  virginica       0          2        49
  • The same result for this particular example

Visualize QDA Results

Code 
partimat(Species ~ ., data = iris, method = "qda")

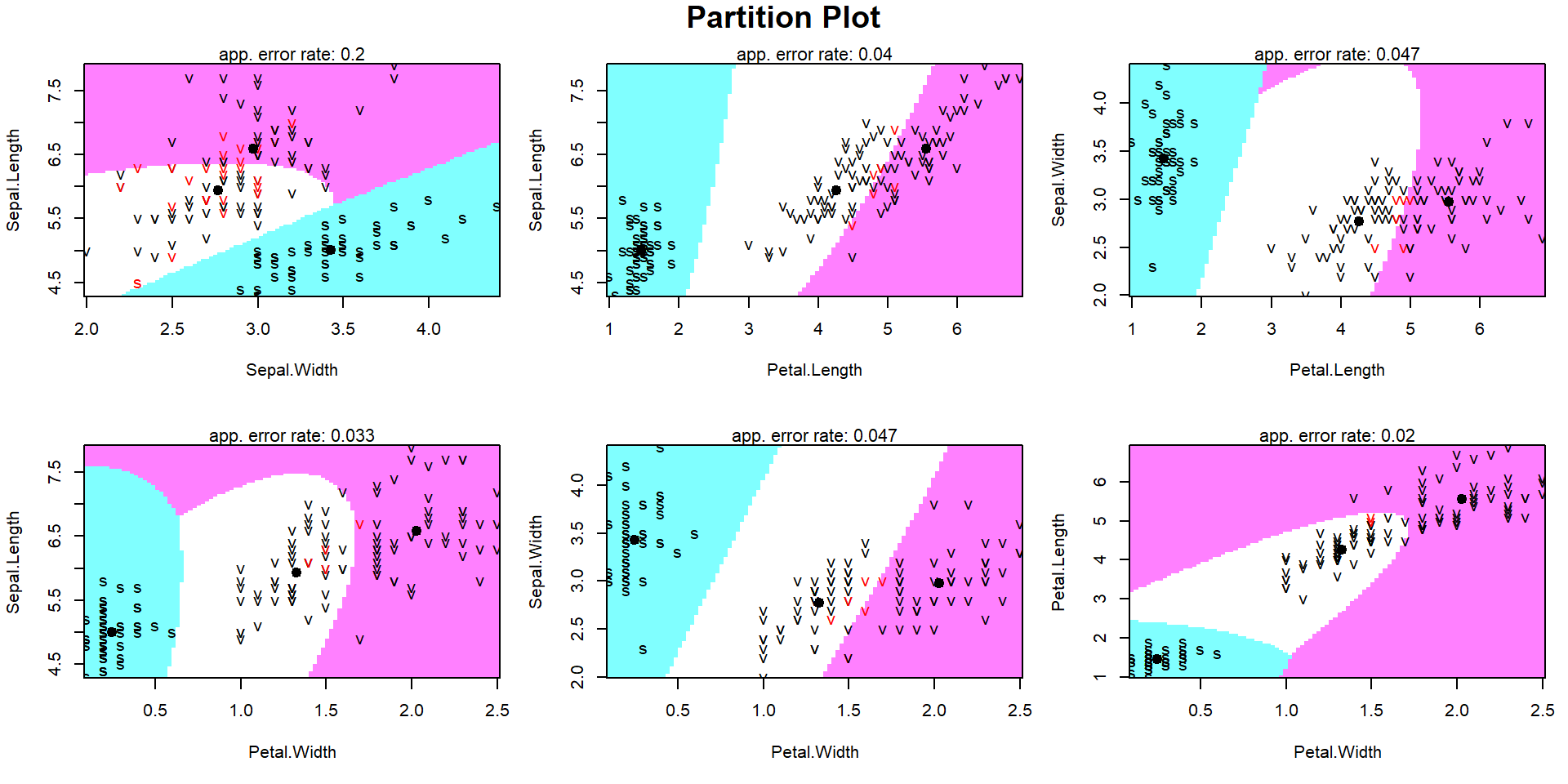
Visualize LDA Results

Code 
partimat(Species ~ ., data = iris, method = "lda")

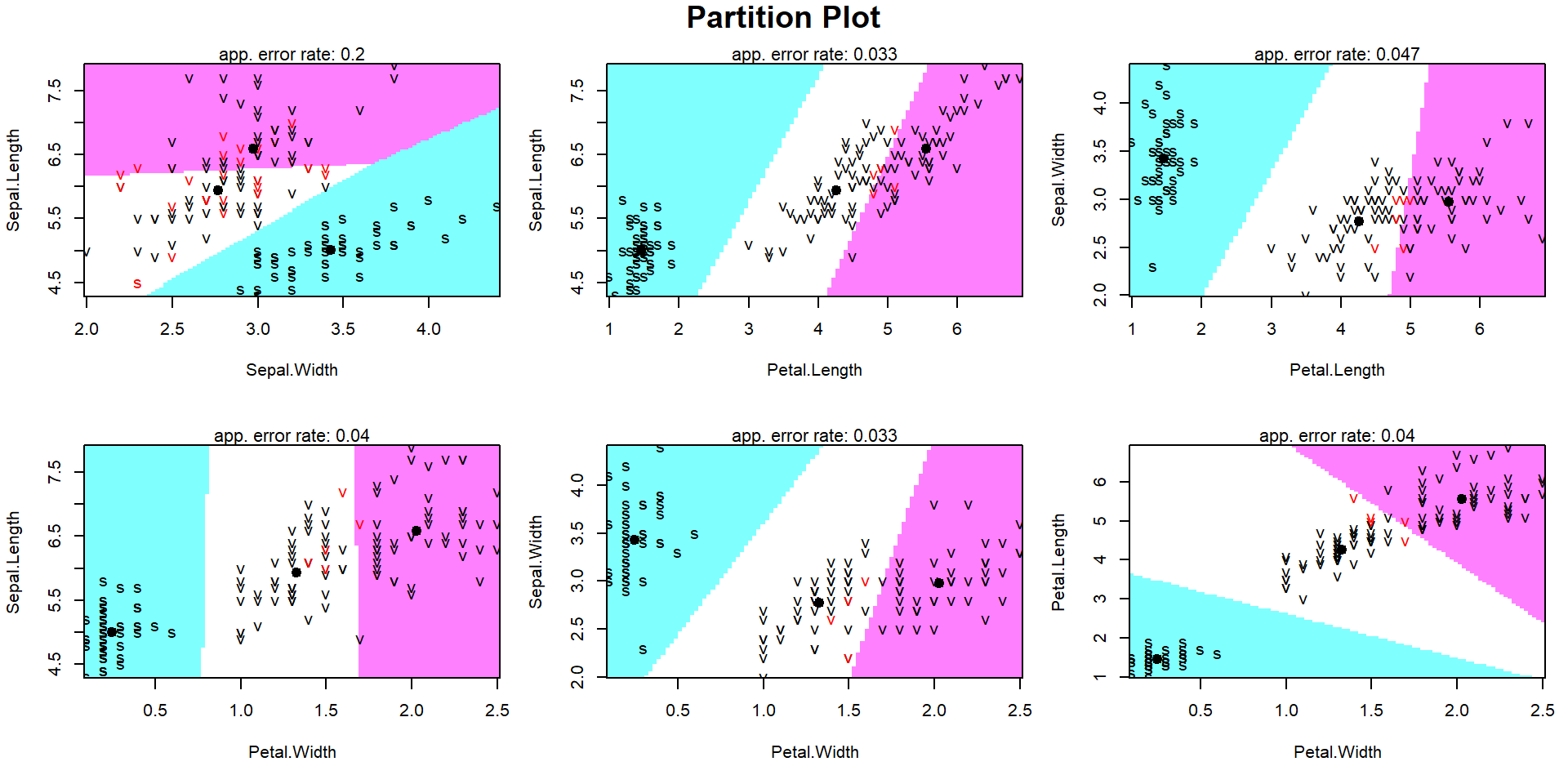
Decision Theory

Cost and Prior Probabilities

  • In practice, different types of errors have different costs
  • Prior probabilities are often known but we haven’t discussed how to use them
  • Goals:
    • When different errors have the same cost, we look for a classification rule that minimizes the probability of misclassification
    • When different errors cost differently, we want to find a classification rule that minimizes the total cost

Equal Costs

Minimize Probability of Misclassification

  • Notations:
  • \(X\): data
  • \(Z\): true class. It is binary, i.e., \(Z=1\) or \(Z=0\)
  • \(P(Z=1)=\pi\): prior probability, known
  • \(\delta(x)\): decision function / classifier
    • \(\delta(x)=1\): allocate \(x\) to group 1
    • \(\delta(x)=0\): allocate \(x\) to group 0

Risk and Posterior Risk

  • Risk of a classifier \(\delta\) \[\begin{aligned} R(\delta, z)&=\Pr [\delta(X)\not= Z|Z=z]=\mathbb E_{X|z} [\mathbb I_{\delta(X)\not= Z}|Z=z]\\ &=\left\{ \begin{array}{cc} \Pr[\delta(X)=0|z=1] & \mbox{ if } z=1\\ \Pr[\delta(X)=1|z=0] & \mbox{ if } z=0 \end{array}\right. \end{aligned}\]

  • The posterior risk of \(\delta\) \[\begin{aligned} PR(\delta(x)) &= \Pr[\delta(x)\not= Z|x]=\mathbb E_{Z|x} [\mathbb I_{\delta(X)\not= Z}|X=x]\\ &=\left\{ \begin{array}{cc} \Pr[Z=0|x] & \mbox{ if } \delta(x)=1\\ \Pr[Z=1|x] & \mbox{ if } \delta(x)=0 \end{array}\right. \end{aligned}\]

Bayes Risk

  • Bayes risk \(B(\delta)=\Pr [\delta(X)\not= Z]\).

  • Note that \[B(\delta)=\Pr [\delta(X)\not= Z]=\mathbb E_{XZ} [\mathbb I_{\delta(X)\not= Z}]=E_X[PR(\delta, X)]=E_Z[R(\delta, Z)]\]

  • Rewrite the Bayes risk \[\begin{aligned} B(\delta) &=\Pr [\delta(X)\not= Z]\\ &=\Pr [\delta(X)=1, Z=0] + \Pr [\delta(X)=0, Z=1]\\ &=\Pr [\delta(X)=1| Z=0]\Pr[Z=0] + \Pr [\delta(X)=0| Z=1] \Pr[Z=1]\\ &=\pi \Pr [\delta(X)=0| Z=1]+ (1-\pi)\Pr [\delta(X)=1| Z=0] \end{aligned}\]

  • The above expression is baesd on the fact \[B(\delta)=\mathbb E_{XZ} [\mathbb I_{\delta(X)\not= Z}]\]

Bayes Classification Rule

  • Want to find \(\delta^*\) that minimizes \(B(\delta)\)
  • Claim 1: the \(\delta^*\) that minimizes \(PR(\delta(x))\) also minimizes \(B(\delta)\)
    • This is because \(B(\delta)=\mathbb E[PR(\delta(X)]\ge \mathbb E[PR(\delta^*(X)]=B(\delta^*)\)]
  • Need to find \(\delta^*\) that minimizes \(PR(\delta(x))\). It can be shown that

\[\delta^*(x)=\left\{ \begin{array}{cc} 1 & \mbox{ if } \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}>1\\ 0 & \mbox{ if } \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}<1 \end{array}\right.\]

  • Skip next slide if you are not interested in the proof

The Classifier that Minimizes Posterior Risk

  • Recall that \[PR(\delta(x)=0)=\Pr(Z=1|x), PR(\delta(x)=1)=\Pr(Z=0|x)\]
  • Therefore, we \(\delta^*(x)\) should be 1 if \[\begin{aligned} PR(\delta(x)=0)>PR(\delta(x)=1) &\Leftrightarrow \Pr(Z=1|x)> \Pr(Z=0|x)\\ &\Leftrightarrow \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}>1 \end{aligned}\]

The Bayes Classificatin Rule

  • We say \(\delta^*(x)\) is the Bayes classification rule \[\delta^*(x)=\left\{ \begin{array}{cc} 1 & \mbox{ if } \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}>1\\ 0 & \mbox{ if } \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}<1 \end{array}\right.\]

  • Computation \[\begin{aligned} \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)} & \overset{\mbox{Bayes' theorem}} = \frac{\frac{f(x|z=1)\Pr(Z=1)}{f(x)}}{\frac{f(x|z=0)\Pr(Z=0)}{f(x)}}\\ & = \frac{f(x|z=1)}{f(x|z=0)}\frac{\pi}{1-\pi} \end{aligned}\]

  • A short review of Bayes’ theorem is on next slide. Feel free to skip if you are very familiar with it already

Bayes’ Theorem

  • Read this slide if you would like to review Bayes’ theorem
  • Let \(A\) and \(B\) be two events.
  • Bayes’ theorem says \[\Pr(B|A) = \dfrac{\Pr(A, B)}{\Pr(A)}=\dfrac{\Pr(A|B)\Pr(B)}{\Pr(A)}\] where \(\Pr(A,B)\) means the joint probability that both \(A\) and \(B\) occur. We can use alternative expressions such as \(\Pr(A \text{ and } B)\) and \(\Pr(A \cap B)\).

Example 1: Univariate

  • Let’s consider a univariate example. Suppose that the population consists for two underlying populations
    • Population 1 with \(\pi\) probability and \(N(\mu_1=1, \sigma^2=0.25)\)
    • population 0 with \(1-\pi\) probability and \(N(\mu_0=0, \sigma^2=0.25)\)
  • Would like to allocate \(x=0.8\)
  • According to Bayes classification rule, we need to compute

\[\begin{aligned} \frac{f(x|z=1)\pi}{f(x|z=0)(1-\pi)} &=\frac{f(x|\mu_1=1,\sigma^2)\pi}{f(x|\mu_0=0, \sigma^2)(1-\pi)}\\ &=\frac{\frac{1}{\sigma\sqrt{2\pi}}exp\{-\frac{1}{2\sigma^2}(x-1)^2\}} {\frac{1}{\sigma\sqrt{2\pi}}exp\{-\frac{1}{2\sigma^2}(x-0)^2\}}\frac{\pi}{1-\pi}\\ &= exp\{\frac{1}{2\sigma^2} (2x-1) \}\frac{\pi}{1-\pi} \end{aligned}\]

Example 1: Univariate

  • The classification boundary is \[\begin{aligned} exp\{\frac{1}{2\sigma^2} (2x-1) \} =(1-\pi)/\pi &\Leftrightarrow \frac{1}{2\sigma^2} (2x-1)=log((1-\pi)/\pi)\\ &\Leftrightarrow x=\sigma^2 log((1-\pi)/\pi)+0.5 \end{aligned}\]

  • The boundary is linear!

    • If \(\pi=0.5\), the boundary is \(x=0.5\), we classify \(x=0.8\) to class 1.
    • If \(\pi=0.7\), the boundary is \(x=0.288\), we classify \(x=0.8\) to class 1.
    • If \(\pi=0.2\), the bondary is \(x=0.846\), we classify \(x=0.8\) to class 0.

Example 1: Density and Classification Boundary

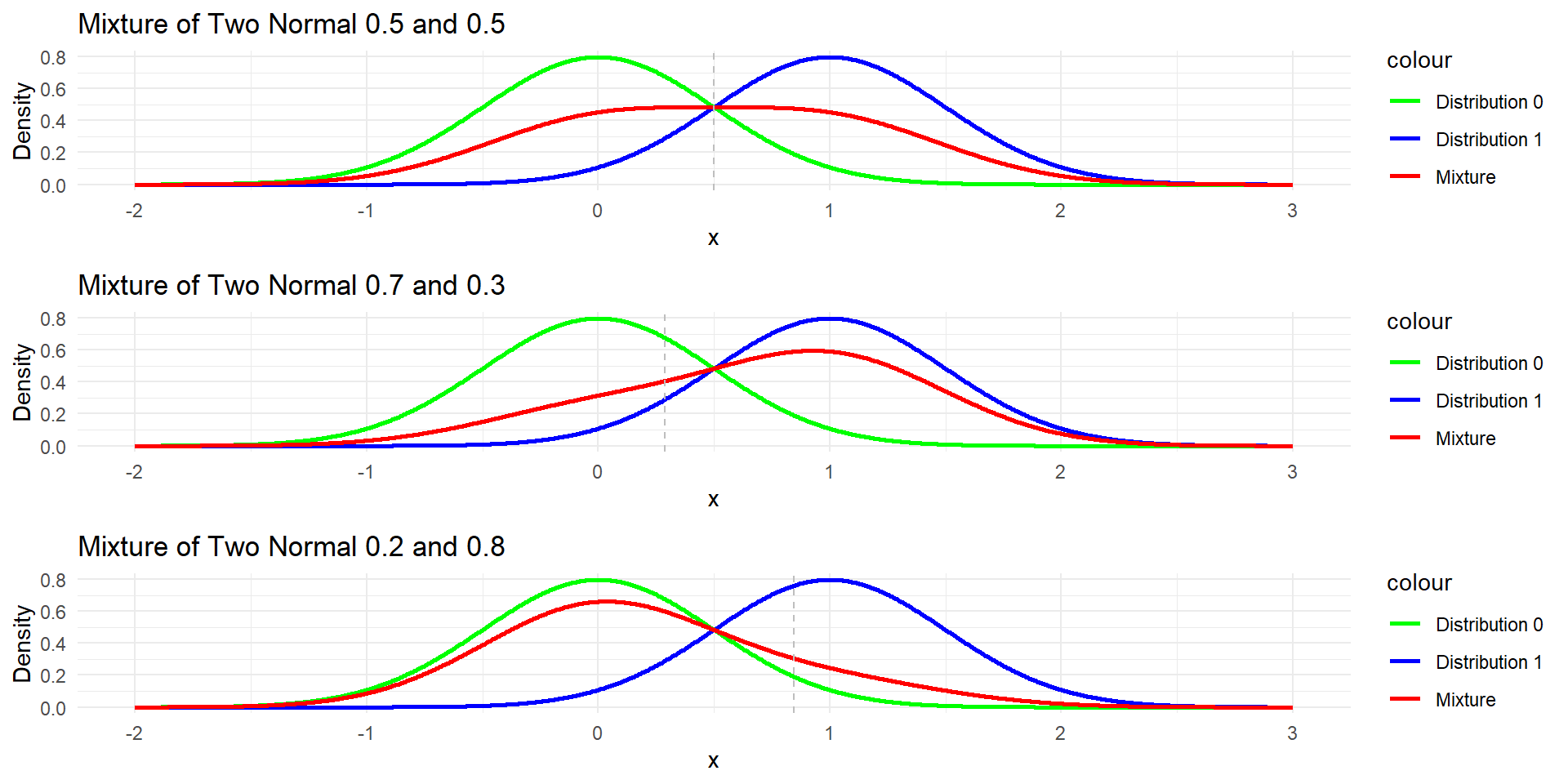
Example 2: Multivariate

  • For a two-class problem, the classification boundary by Bayes’ classification rule is \[\frac{f(x|z=1)\pi}{f(x|z=0)(1-\pi)}=1\\ \Leftrightarrow log(\frac{f(x|z=1)}{f(x|z=0)})=log(\frac{1-\pi}{\pi})\]

Bayes’ Classification under Equal Covariance

  • Suppose the two underlying distributions are \(N(\boldsymbol\mu_1, \boldsymbol \Sigma)\) and \(N(\boldsymbol\mu_2, \boldsymbol \Sigma)\).

  • The boundary is \[-\frac{1}{2}(x-\boldsymbol\mu_1)^T \boldsymbol\Sigma^{-1}(x-\boldsymbol\mu_1) + \frac{1}{2}(x-\boldsymbol\mu_1)^T \boldsymbol\Sigma^{-1}(x-\boldsymbol\mu_1)\\ =log(\frac{1-\pi}{\pi})\] which is equivalent to

\[(\boldsymbol\mu_1 -\boldsymbol\mu_2)^T \boldsymbol\Sigma^{-1}x = (\boldsymbol\mu_1 -\boldsymbol\mu_2)^T\boldsymbol\Sigma^{-1}\frac{\boldsymbol\mu_1 + \boldsymbol\mu_2}{2} + log(\frac{1-\pi}{\pi})\]

Bayes’ Classification under Equal Covariance

  • In practice, we substitute the unknown parameters by their estimates \[(\bar {\mathbf X}_{1.} -\bar {\mathbf X}_{2.})^T\boldsymbol\Sigma^{-1}x = (\bar {\mathbf X}_{1.} -\bar {\mathbf X}_{2.})^T \boldsymbol\Sigma^{-1}\frac{\bar {\mathbf X}_{1.} + \bar {\mathbf X}_{2.}}{2} + log(\frac{1-\pi}{\pi})\]

  • Recall that in LDA the linear boundary is \[a^Tx=a^T\frac{\bar {\mathbf X}_{1.} + \bar {\mathbf X}_{2.}}{2}\] Therefore, Bayes’ classification is the same as the LDA when \(\pi=1/2\).

  • Similarly, in a g-class problem, LDA is the same as Bayes classification under the assumptions (1) multivariate normality, (2) equal covariance, and (3) uniform prior probabilities.

Connection with Logistic Regression

  • The ratio of posterior risk is \[\frac{\Pr(Z=1|x)}{{\Pr(Z=0|x)}}\]
  • It is also called the odds ratio. A logistic regression models the log-odds as a linear function of the covariates.
  • The LDA under the Bayes rule computes the ratio of the posterior risk.

Connection with Logistic Regression

  • In both approaches, the decision function is a linear function of the covariates.
  • They also give similar results.
  • The two approaches were derived from different models with different assumptions.
    • Logistic regression models the behavior of a binary response variable given covariates.
    • LDA models the multivariate behavior of covariates given the class labels.
  • If MVN is not satisfied, LDA is not a good approximation to the posterior risk. In this situation, logistic regression is a better choice.

Example 3: Univariate, Unequal Variance

  • Again, consider a univariate example. This time we relax the assumption of equal variance
  • Suppose that the population consists for two underlying populations
    • Population 1 with \(\pi\) probability and \(N(\mu_1=1, \sigma_1^2=0.25)\)
    • population 0 with \(1-\pi\) probability and \(N(\mu_0=0, \sigma_2^2=1)\)
  • Would like to allocate \(x=0.8\)

Example 3: Univariate, Unequal Variance

  • According to Bayes classification rule, we need to compute \[\begin{aligned} \frac{f(x|z=1)\pi}{f(x|z=0)(1-\pi)} &=\frac{f(x|\mu_1=1,\sigma_1^2)\pi}{f(x|\mu_0=0, \sigma_0^2)(1-\pi)}\\ &=\frac{\frac{1}{\sigma_1\sqrt{2\pi}}exp\{-\frac{1}{2\sigma_1^2}(x-1)^2\}} {\frac{1}{\sigma_0\sqrt{2\pi}}exp\{-\frac{1}{2\sigma_0^2}(x-0)^2\}}\frac{\pi}{1-\pi}\\ &= exp\{(\frac{1}{2\sigma_0^2}-\frac{1}{2\sigma_1^2})x^2 + \frac{x}{\sigma_1^2}-\frac{1}{2\sigma_1^2}\} \frac{\pi}{1-\pi}\frac{\sigma_0}{\sigma_1} \end{aligned}\]

Example 3: Univariate, Unequal Variance

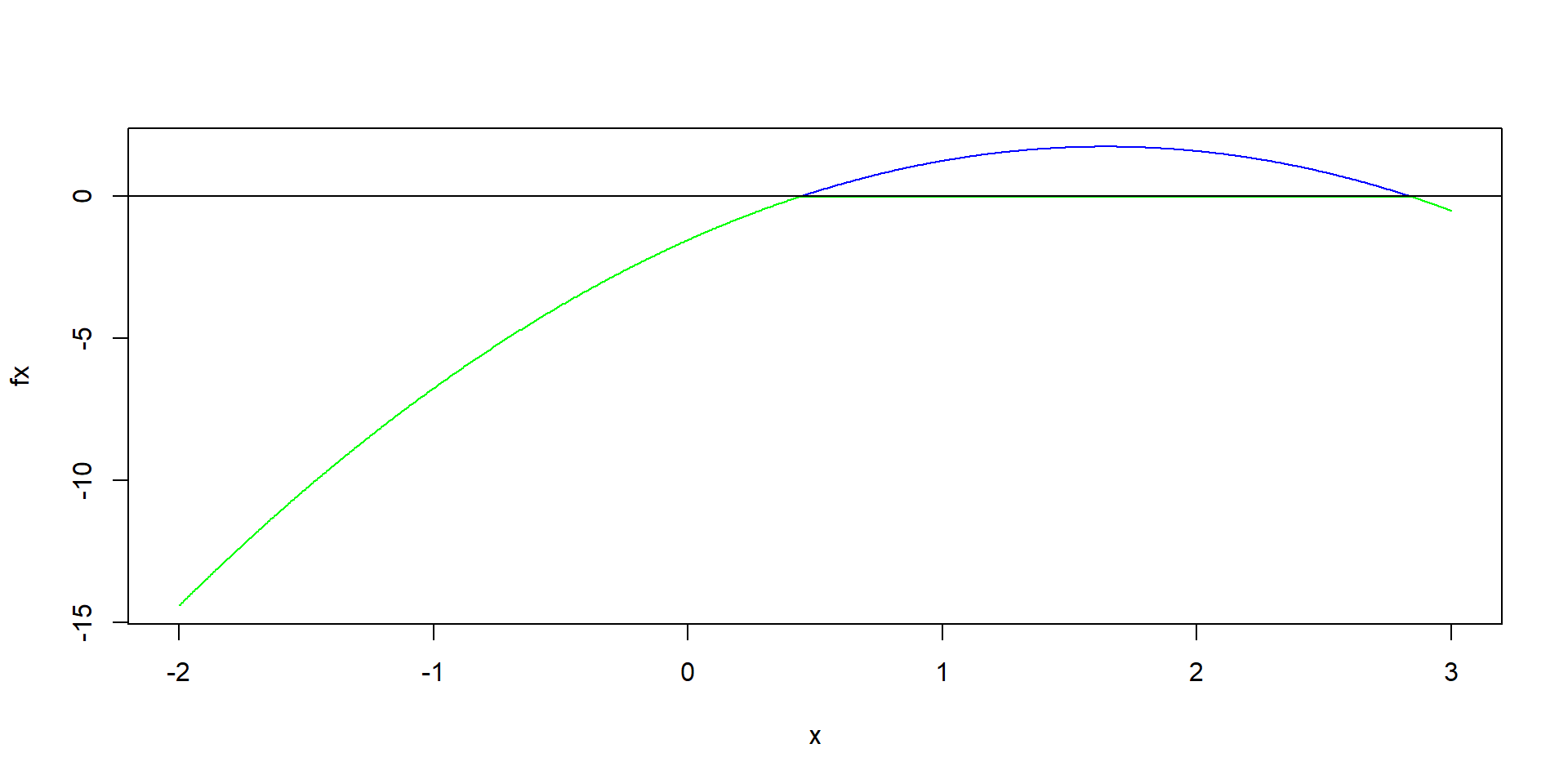
  • The classification boundary is \[(\frac{1}{2\sigma_0^2}-\frac{1}{2\sigma_1^2})x^2 + \frac{x}{\sigma_1^2}-\frac{1}{2\sigma_1^2}=log[ \frac{1-\pi}{\pi}\frac{\sigma_1}{\sigma_0}] \]

  • It is quadratic!

Example 3: Univariate, Unequal Variance

Code 
mean1 <- 1
var1 <- 0.25
mean0 <- 0
var0 <- 0.64
weight1 <- 0.5
weight0 <- 1 - weight1

# doesn't seem to be correct
x <- seq(-2, 3, length.out = 1000)
fx=(1/var0 - 1/var1)/2*x^2 + x/var1 - 1/2/var1 - log(weight0*sqrt(var1)/weight1/sqrt(var0))
plot(x, fx, type="n")
lines(x[fx>0], fx[fx>0], col="blue")
lines(x[fx<0], fx[fx<0], col="green")
abline(h=0)

Example 3: Univariate, Unequal Variance

Unequal Costs

Risk and Cost

  • Different types of misclassifications might cost differently
  • Let \(L(\delta(x), z)\) denote the cost function
  • Let \(C(1|0)=L(1, 0)\), the cost of misclassifying 0 to 1
  • Let \(C(0|1)=L(0, 1)\), the cost of misclassifying 1 to 0
  • The Risk and Bayes risk need to be revised accordingly

Risk and Posterior Risk

  • Risk of a classifier \(\delta\) \[R(\delta, z)=\mathbb E_{X|Z=z} [L(\delta(X), z)]=\left\{ \begin{array}{cc} C(0|1)\Pr[\delta(X)=0|z=1] & \mbox{ if } z=1\\ C(1|0)\Pr[\delta(X)=1|z=0] & \mbox{ if } z=0 \end{array}\right.\]

  • The posterior risk of \(\delta\) \[\begin{aligned} PR(\delta(x)) &= \mathbb E_{Z|x}[L(\delta(x), Z)]\\ &=\left\{ \begin{array}{cc} C(1|0)\Pr[Z=0|x] & \mbox{ if } \delta(x)=1\\ C(0|1)\Pr[Z=1|x] & \mbox{ if } \delta(x)=0 \end{array}\right. \end{aligned}\]

Bayes Risk

  • Bayes risk \[B(\delta)=\mathbb E_{XZ} [L(\delta(X), Z)]\]
  • Rewrite the Bayes risk

\[\begin{aligned} B(\delta) &=\mathbb E_{XZ} [L(\delta(X), Z)]\\ &=L(\delta(X)=1, Z=0)\Pr[\delta(X)=1, Z=0] + L(\delta(X)=0, Z=1)[\delta(X)=0, Z=1]\\ &=C(1|0)\Pr [\delta(X)=1, Z=0] + C(0|1)\Pr [\delta(X)=0, Z=1]\\ &=C(1|0)\Pr [\delta(X)=1| Z=0]\Pr[Z=0] + C(0|1)\Pr [\delta(X)=0| Z=1] \Pr[Z=1]\\ &=C(0|1)\pi \Pr [\delta(X)=0| Z=1]+ (1-\pi)C(1|0)\Pr [\delta(X)=1| Z=0] \end{aligned}\]

Bayes Classification Rule with Unequal Costs

  • Use a derivation similar to the equal cost situation, we can show that the Bayes classification rule is

\[\begin{aligned} &PR(\delta(x)=0)>PR(\delta(x)=1) \\ &\Leftrightarrow C(0|1)\Pr(Z=1|x)> C(1|0)\Pr(Z=0|x)\\ &\Leftrightarrow \frac{\Pr(Z=1|x)}{\Pr(Z=0|x)}>\frac{C(1|0)}{C(0|1)}\\ &\Leftrightarrow \frac{f(x|z=1)}{f(x|z=0)}>\frac{C(1|0)}{C(0|1)}\frac{1-\pi}{\pi} \end{aligned}\]